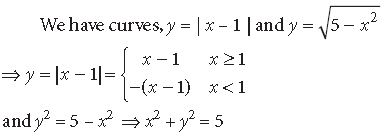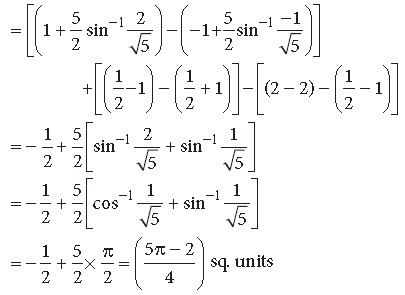Please refer to below Exam Question for Class 12 Mathematics Chapter 8 Application of Integrals. These questions and answers have been prepared by expert Class 12 Mathematics teachers based on the latest NCERT Book for Class 12 Mathematics and examination guidelines issued by CBSE, NCERT, and KVS. We have provided Class 12 Mathematics exam questions for all chapters in your textbooks. You will be able to easily learn problems and solutions which are expected to come in the upcoming class tests and exams for standard 10th.

Chapter 8 Application of Integrals Class 12 Mathematics Exam Question

All questions and answers provided below for Exam Question Class 12 Mathematics Chapter 8 Application of Integrals are very important and should be revised daily.

Exam Question Class 12 Mathematics Chapter 8 Application of Integrals

Short Answer Type Questions

Question. Find the area of the region included between the parabola 4y = 3x² and the line 3x – 2y + 12 = 0.
Answer.

Question. Using integration, find the area of the region bounded by the curves :
y = |x + 1| + 1, x = – 3, x = 3, y = 0
Answer. Here, y = |x + 1| +1

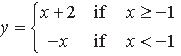
We now draw the lines : y = 0, x = 3, x = –3 and
y = x + 2 if x ≥ -1 ….(i)           y = − x if x < – 1  ….(ii)
Lines (i) and (ii) intersect at (– 1, 1)

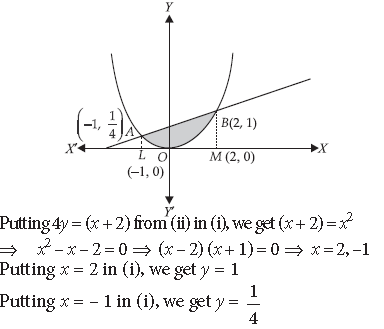
Question. Using integration, find the area bounded by the curve x² = 4y and the line x = 4y – 2.
Answer. The given curve is x² = 4y                   …(i)
The given line is x = 4y – 2                              …(ii)

Question. Find the area of the region bounded by the parabola y = x² and y = |x|.
Answer. The given curves are y = x²                 …(i)

Their points of intersection are A (1, 1), O(0, 0) and B (–1, 1).
In view of symmetry, the required area

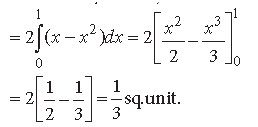
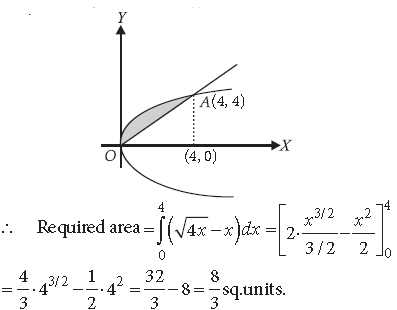
Question. Using integration, find the area of the region enclosed by the curves y² = 4x and y = x.
Answer. The given curves are y² = 4x, y = x
They intersect at O(0, 0) and A (4, 4).

Question. Prove that the curves y² = 4x and x² = 4y divide the area of the square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Answer.

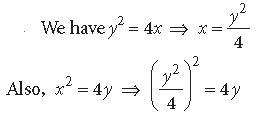
⇒ y⁴ = 64y ⇒ y = 0 or y = 4
When y = 0, x = 0 and when y = 4, x = 4
So, the points of intersection are O(0, 0) and P(4, 4)
Let A₁, A₂, A₃ be the area denoted in the figure.
We need to prove A₁ = A₂ = A₃.

Thus y² = 4x and x² = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.

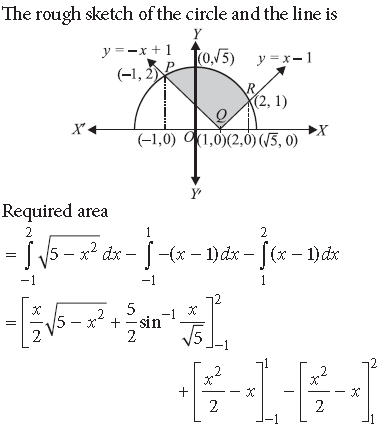
Question. Using integration, find the area of the region bounded by the curves
Answer.

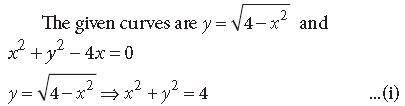
This represents a circle with centre O(0, 0) and radius = 2 units.
x² + y² – 4x = 0 ⇒(x – 2)² + y² = 4 …(ii)
This represents a circle with centre B(2, 0) and radius = 2 units.
Solving (i) and (ii), we get (x – 2)² = x² ⇒ x = 1
∴ y² = 3 ⇒ y = ± √3

Question. Using integration, find the area of the triangular region whose sides have equations y = 2x + 1, y = 3x + 1 and x = 4.
Answer. The given lines are y = 2x + 1 …(i)
y = 3x + 1 …(ii) and x = 4 …(iii)
Solving (i) and (ii), we get x = 0, y = 1
Solving (ii) and (iii), we get x = 4, y = 13
Solving (iii) and (i), we get x = 4, y = 9
∴ Required area = area (ΔABC)
= area (OABD) – area (OACD)

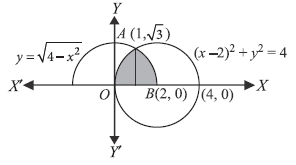
Question. Using integration, find the area of the triangle ABC, coordinates of whose vertices are A(4, 1), B(6, 6) and C(8, 4).
Answer. Here A(4, 1), B(6, 6) and C(8, 4).

Question. Find the area of the circle 4x² + 4y² = 9 which is interior to the parabola x² = 4y.
Answer. The given circle is 4x² + 4y² = 9 i.e.
x² + y² = 9/4 which has centre (0, 0) and radius 3/2.
The given parabola is x2 = 4y which is symmetrical about positive y-axis with vertex (0, 0).
Solving both the equations, we get

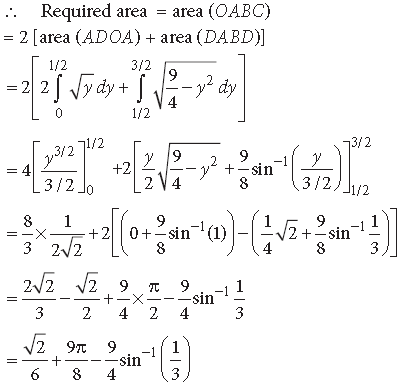
Question. Find the area of the region lying between the parabolas y² = 4ax and x² = 4ay, where a > 0.
Answer. The equations of the curves are
y² = 4ax …(i) and x² = 4ay …(ii)

Question. Using integration, find the area of the region bounded by the triangle whose vertices are (1, 3), (2, 5) and (3, 4).
Answer. Let the points be A(1, 3), B(2, 5) and C(3, 4)
Equation of AB is y – 3 = 2 (x – 1) ⇒ y = 2x + 1
Equation of BC is y – 5 = – 1(x – 2) ⇒ y = 7 – x

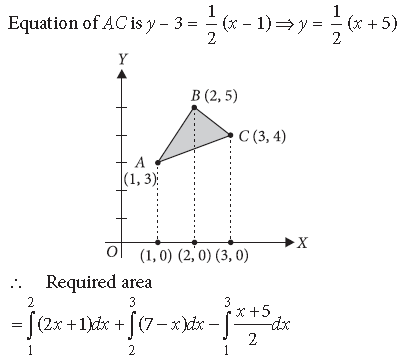
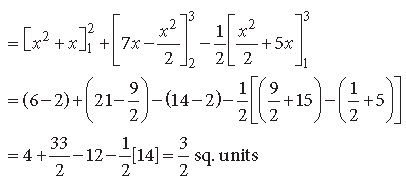
Question. Using integration, find the area lying above x-axis and included between the circle x² + y² = 8x and the parabola y² = 4x.
Answer. We have x² + y² = 8x and y² = 4x
Now, x² + y² = 8x ⇒ (x – 4)2 + y² = (4)2
The centre of circle is (4, 0) and radius is 4.
The point of intersection of circle and parabola are 0(0, 0) and A(4, 4) above x-axis.

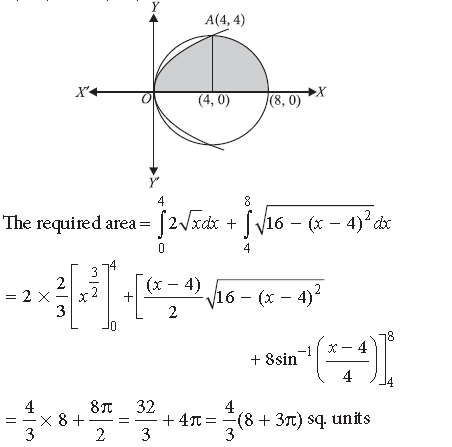
Long Answer Type Questions

Question. Using integration, find the area of the region enclosed between the two circles x² +y² = 4 and (x – 2)² + y² = 4.
Answer. The given circles are
C₁ : x² + y² = 4 …(i) and C₂: (x – 2)² + y² = 4 …(ii)
Eliminating y from (i) and (ii), we get
4 – x² = 4 – (x – 2)² ⇒ 4x = 4 ⇒ x = 1
Putting x = 1 in (i), we get y² = 3 ⇒ y = ± 3
⇒ Points of intersection of the two circles are A(1, 3) and B(1, − 3)

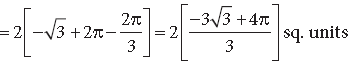
Question. Using integration, find the area of the triangle formed by positive x-axis and tangent and normal to the circle x² + y² = 4 at (1, √3) .
Answer. Given equation of circle is x² + y² = 4
Differentiate w.r.t. ‘x’ on both sides, we get

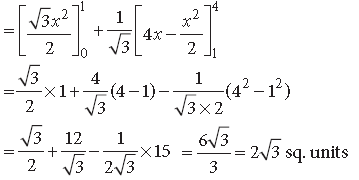
Question. Using integration, find the area of the following region :

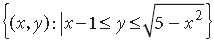
Answer.